
�@���w�Ō����Ȃ낤
�@���E�G��
�@���P����ł�������u��
| |
�����F�펚 |
||||||||
| Boys & girls, be KASHICO. It's cool. KASHICO means a person who is wise, clever, intelligent and so on. This site makes you KASHICO�D | |||||||||
| By Kano Origuchi | |||||||||
| �l�d�m�t�@�@�g�n�l�d | �r�������` �@���w�Ō����Ȃ낤 |
�r�������a �@���E�G�� |
���w���w�u���Q�O�Q�O/�X�` �@���P����ł�������u�� |
���ވē� | |||||
| |
�֑����������܂������Ȃ��̂ł��e�͊肢�܂��B�@�@�@�w�͂�����.�D�b�n�l�i�q�j | |
|
| �ڎ��i�ŐV���j �O�O�X�@���� �ׂ̕��������� �O�O�W�@���ՂɁA����ɈՂ�����������A�ł���悤�ɂȂ�Ƃ͌���Ȃ� �O�O�V���ꂪ�ʂ����āA�P�A���X�~�X�Ȃ̂��@�V/�Q�Snew �O�O�U�@���x�߁@�V�˂�ڎw�� �O�O�T�@��_�˔j �O�O�S�@���P�M���b�v�͏��w�Z����n�܂��Ă���A�����C�����Ȃ������� �O�O�R�@�f�t�H���g���[�h�l�b�g���[�N �O�O�Q�@������ڎw���Ȃ��� �O�O�P�@���̕� �O�O�O�@���̃T�C�g�̃X�^�C�� |
�O�O�O | ���̃T�C�g�̃X�^�C�� �@�ŏ��Ɂu�T�C�g�����������R�v�𗝉����Ă�����Ă���̕����������肷��̂����A�ƂĂ������Ȃ肻���ŒǁX�����Ă������Ǝv���B���E�������Ď�ɂ��������Ȏ��m�����A�������猩����i�F�Ɖ����������̂����`��������肪�����B �@�o�ς�Љ�S�ʂɓn���ē��{�̃V�X�e���������Ȃ炻��ł������A���������ŕs����N�����Ă���悤���B�Г��ٕς��N�������Ƃ��ɁA���̂ق���т��\�Ɍ���Ă���B �@�ŋ߂ł͋���Ɋւ��邱�ƂɌ���ƁA�R���i�ЂŃI�����C�����Ƃ����悤�ɂ�OECD�����������@��̎g�p�����ʼn��ʂɋ߂����Ƃ����������B�܂��A�t�[�h���X�����ɂȂ��Ă��锽�ʁA�w�Z���H���X�g�b�v����Ɖe�����y�Ԏq�ǂ�������B �@�R���i�Ђ��Ȃ������Ƃ��Ă��A����ɂ͌��݉����Ă��Ȃ��s�������B �@���̕s����������邽�߂Ɂu����ȃX�^�C���Ő��w������Ă�������Ȃ����v�Ƃ�����Ăł���B �@���̃T�C�g�̊Ǘ��҂��l���Ă���s��͎��̂悤�Ȃ��̂��B �@���Ƃ������̂�����̕ω��Ɏ��c����Ă���A����Ă���̂ł͂Ȃ����B�����ɋ��ʂ��Ă���̂��u�n�R�������v���B �@���������闝�R�́A���̓��@�t����ړI���u�𗧂v���Ƃɕ肷���Ă���A���l���ł���\�͂łȂ��Ɣ��f�ł��Ȃ��A��̕�����Ȃ����Ƃ����Ȓm���Ȃǂ��ꎞ�I�ɂ���]���Ɏ��]�T���Ȃ��A�����������ɒ��w�����u����Ă���Ƃ������Ƃ��B �@�u�𗧂m���v�͕���̂������A�Ƃ������̂͐��w�̖��������������X�B�̌��t���B�Ⴆ�Β��w���Ȃ����e�X�g�̓_�����グ�邽�߂����̕�������ɂ�����B�������w���ɂƂ��ē��@�t���Ƃ��Ă͖ڐ�̖ڕW���K�v�����A�ǂ����Ă��₹�ׂ����m���ɂȂ��Ă��܂��B �@�_���Ώd���s���߂���Ƃ���Ȃ��Ƃ��N����B����e�X�g��Ƃ����āA����m�ł͒��w�Z�ŏo���ߋ����ۊǂ��Ă��āA���̐搶�̒S�C�ɂ͂��̖���������B�`�F�[���X��W�J���Ă���m�Ȃ�A�]���Ă����搶�ɑ��Ă͕��C�O�̊w�Z�̂���x�X�������Ƃ����B���ɕ����Ȃł͂قƂ�Ǔ�����肪�ł�炵���B �@���k(�l��)��]������͓̂���B�z���́A�n���́A�ώ@��A�����́A�����́c�@��ϓI�Ȃ��̂͂Ȃ����炾�B�����Ƃ����ϓ_���炢���A�q�ϓI�ȃe�X�g�ƂȂ�B����͎d�����Ȃ��B�������A���l���ł������(�e�X�g�̓_���Ȃ�)�ŕ�����\�͂͂����ꕔ���Ȃ̂��ƐS���Ă������Ƃ�����B�R���i�Ђł̑Ή��́A�����Ƃ��Ċe���̃��[�_�[�������Ă��鋤���͂�z���͂̍����ł��̂��Ǝv���B��������ɗ����������l���B �@�l�ނ͉����N���Ɉ�x��i�����邾�낤�Ƃ����Ă���B�Ƃ������Ƃ́A�}���ɔ��B�������@��ɐl�ނ͂���ɑΉ��ł���Ă��A�����̎d����v�l�̕��@��m���̊l�����@�͂����ȒP�ɕς��Ȃ��ƍl���Ă���B������A�×���肠��w�K�@�ɂ͈Ӗ�������A�l�̔\�͂������o�����@�͂��炩���o�s�����Ă���ƍl���������悢�B�F�m�̍\����]�̋@�\���𖾂���āu����ł��������������Ă����̂��v�Ɣ[���͂ł��Ă��A�V�����w�K�@��������Ƃ͍l���ɂ����B �@�Ⴆ�Ώ������Ƃ�����킯�̕�����Ȃ��܂܊�����N���A�[��(�R�[����)���Ï�����ɂ͈Ӗ�������ƍl����B������Ȃ����́A����̈Ⴄ���̂���U���ɒu���Ă����B��������Ɠ��̒��Ŕ��y���i�ށA�������݂����Ȃ��̂������ĉ��w�������N�����A���ꂪ�ǂ����z����A�~�g�A���n����A�X�����v���甲����c�@�Ƃ������Ƃ��Ǝv���B �@�l�b�g��n�[�h�f�B�X�N��ɖc��ȃA�[�J�C�u���������Ƃ��Ă��A�����w���ɂƂ��āA����Ȃ�̎g�����͂ł��邾�낤���A�����y������\�͂����Ă��˂Ȃ�Ȃ��B �@�Ǐ��S�Ոӎ�������ʂ��A�A�C�f�A���o�Ă���͔̂n��E����E�̏�A�o�J���X�ł͉������Ȃ��A�A���L���f�X���w�E���[�J�Ƌ��̂��A���̗V�т������Ăł�����̂��B �@����ł��̃T�C�g�ł́u�������v���Ȃ邽�߂̃e�[�}���Q�ɍi�����B�u���̕��v���u������ڎw���Ȃ����i�������A�e�X�g�ł͖��_���Ƃ�j�v�ł���B���̃X�^�C����ς���Γ��{�̏����ɂ������������ނ�Ȃ����A�Ƃ����傻�ꂽ��]�������Ē��w���w�ɗՂ�ŗ~�����B |
|
| �O�O�P | ���̕� �@���̕��Ƃ́A�@�@�ܖ������̒����A���ɂł��悭�������@�A�@�������l�����A���������̌����܂ܖ{��ǂ�A�����œ��ɔ[�߂Ă������Ǝv�����m�������̂ǂ����ɒu���Ă����B���Ǝv���Ă��Ȃ����A�����l���Ă悢�B �@�X�B�����łȂ��A�c��`�m�m������������M�O���u�����ɖ��ɗ����̂́A�����ɖ��ɗ����Ȃ��Ȃ�v�Ƃ������t���c���Ă���B�A�E��d����Ō��莎����Ƌ����Ƃ�̂��u�𗧂m����Z�\�v�Ƃ��ĕK�v�����A���w�����߂Ē��w�����炢�܂ł͎����̔\�͂����߂�������Ăق����B �@���オ�ς��A������m����Z�\���ς���Ă���B���Z���w�Ŋw���Ƃ��炢�ňꐶ����Ă������Ƃ����̂́A�����܂�������B�V���ɕ��������A�V���m�����l������K�v�ɔ���ꂽ�Ƃ��̔\�͂��܂��b���Ăق����B �@����e�X�g�̓_�����グ�邽�߂̕��A�v���O���~���O���炪���������ƂȂ�Ɛ��肵�ďm�Ŏn�܂�B�����ɑΉ��������_�Łu���v���ӂށB�v���O���~���O���炪�����̂ł͂Ȃ��B���ۂɂ̓v���O���~���O�I�Ȏv�l�@���e���Ȃɓ�������悤�����A�v���O���~���O����ɂ���Ďq�ǂ������̂ǂ�Ȕ\�͂������o�����Ƃ��Ă���̂��������Ă��Ȃ��B�A���S���Y���H�@�_���I�v�l�H�@����Ȃ��Ƃ͎Z���␔�w�⑼���ȂňȑO���炸���ƖڕW�Ƃ��Ă����B �@��������A�r�������`�Ŏq�ǂ��̎��Ԃ�m���Ăق����B�q�ǂ������������T���Ă���̂��A����g�ɂ����������̂��A�ǂ�Ȕ\�͂��J�Ԃ��������̂���������x�������A�D�揇�ʂ�������͂����B �@���オ�ς���Ă��A�V�����@�킪�o�Ă��Ă��A�`�h�ɂ���Ďd�����ω����Ă��A���ɓV�Ђŋ@�킪�S���g���Ȃ��Ȃ����Ƃ��Ă��ʗp����̂��u���̕��v���B �@�������Ă�����������Ȃ��Ƃ��ɁA�v�l��~�����ɑO�ɐi�߂�B���̃T�C�g�ł́A���w���w�̖���ʂ��āA�u�ǂ�����ē��ɂƂ�����v�u�ܗ������łǂ��s�����邩�v�c���l���Ă��������B�������������@�͐��w�����ɒʗp����킯�ł͂Ȃ��B���ɂł��悭�������@�Ȃ̂ł���B |
||
| �O�O�Q | ������ڎw���Ȃ��� �@������ڎw���Ȃ����Ƃ́A�������ڂ�ڎw�����ł͂Ȃ��B�����Ԃ�Z�k���ė]�������Ԃ�Ǐ���X�|�[�c�A�����̂��镪��ɐU�������B�������x��ł������B���̂��߂̕��@�Ǝv���Ă��炢�����B�������������Z�̓������͖��_��ڎw���B �@���w���ɐ��w�������Ă����O�A���N�̓�����������(�{)�������B���̂Ƃ����ۂɎg���Ă���m����Z�p�͂���Ȃɑ����Ȃ��B���w�̋��ȏ��ƎZ���ŏ\���ł���B�w�K�w���v�͈̂̔͊O����o�肳��鎄����֍Z�����邪�A�������邩�A�܂��͑O�q�̒m���E�Z�p�v���X�m�b�őΉ�����B������Ȗ��ł��A���ǂ͊�{�̑g�ݍ��킹������ł���B�ǂ����Ă����ԓ��ɉ����������Ȃ��悤�Ȗ������܂ɂ��邪�A�������ĉ����K�v���Ȃ��B�ɂȂƂ��ɓ��̑̑��ɂƂ��Ă����悢�B �@�p���[�g�̖@��(�o�����ł������Ƃ������_�ł͂Ȃ���)�Ƃ������̂�����B�ʖ��u�W�O�p�[�Z���g�E�Q�O�p�[�Z���g�̖@���v�Ƃ����B�Ⴆ����H��ŏo��s�Ǖi�̌����̏�ʂQ�O�p�[�Z���g���Ȃ����Εs�Ǖi���W�O�p�[�Z���g��������B�R�قǂ̋@�\������X�}�[�g�t�H���ŁA�Q�O�p�[�Z���g�̂悭�g���@�\�łW�O�p�[�Z���g�̓J�o�[�ł���E�E�E�ȂǁA���������g����������B �u�悭����⎑�i�����̕��@�ŁA�o����̓��d�v�ȂQ�O������������A�W�O�_���Ƃ��v�Ƃ����g����������邪�A���̃T�C�g�̃X�^�C���͂���Ƃ͍l�������Ⴄ�B �@���̃T�C�g�Ŏg���m����Z�p�́u��{�̒m���E�Z�p�v�ł����Č��ʓI�ɑS�̂̂Q�O�����炢�ɂ����邩������Ȃ����A�W�O�_��ڎw���̂ł͂Ȃ��~�����Ė��_��ڎw���B���_�̌��ƂȂ�L�[���[�h���u�������v�ł���B�m�b��G�b�W�A�����̎����Ă���m�����g�����Ȃ��A�g������͉̂��ł��g���c�����̎����Ă��鎑������������B �@�������������̂͊�{�I�Ɍl�̂��̂��B�Ȃ��Ȃ�A������Ƃł��y���Čv�Z�������A�킴�킴��肭�ǂ������������Ȃ��Ă���������p����c�Ƃ������ςݏd�˂��u�������v�̒����ƂȂ�B �@�������A����Ȃ��Ƃ��v�����Ď��s�Ɉڂ����k�͂���Ȃɂ͂��Ȃ��B�܂��߂ŋ��B�����ꂽ����������O���̂�|����B�ω����ōU�߂��Ɋm���Ȃ��̂ł���B �u�������v�Ɩ��������͂��Ȃ��B������ݏo�������k���[�������Ƃ��u�����������ƂȂ̂��v�Ƌ��ȏ��Ȃǂɏ�����Ă�������̈Ӗ������߂ĕ�����B �@���̃T�C�g�ł́A�����������Ƃ������Ȃ���i�߂�B���̂��߂��ƁA������x�O��������Ȃ�A���R�ɂȂ鎞�Ԃ����o�����߂ł���B |
||
| �O�O�R | �f�t�H���g���[�h�l�b�g���[�N �@�f�t�H���g���[�h�l�b�g���[�N�Ƃ́u��������́A�ځ[���Ƃ��Ĕ]���x�߂�A��������Ό����Ȃ��Ă���v�Ƃ������@�̓��������Ă����]�_�o�̃l�b�g���[�N�̂��Ƃ��B �@�������A�N���ځ[���Ƃ��Ă���Ԃɂ��A�ӎ����Ŕ]�͖җ�Ɏd�������Ȃ��Ă���B���Ԋw�Z�Ŋw���Ƃ��J��Ԃ�����A�������Â炢�Ƃ�������Ă���Ă���B����ɂ��ƁA�N�����������Ă��鎞�ԂɎg����G�l���M�[�̂Q�O�{���g���Ă���炵���B �@�]�̈ӎ����̓������y�����Ă͂����Ȃ��B�������A�ځ[���Ƃ���̂����߂����v������A�ɂɂȂ�̂���������{�l�͑����̂��낤�B���s�͂������������̂�����ƁA�����݂̃X�P�W���[���Ŗڈ�t���ĉ��Ƃ����A���{�l�̐�����\����^��݂����Ȃ��̂��������B �@���ꂪ���ɂȂ�ƁA���k�͂炢�B�̂ɔ�ׂď��X�ɍs���Ζ��W�̂������͎R�قǂ��邵�i�w�Z�Ŕz���镛���ނŏ\���Ȃ̂����j�m���������Ă���B�u�q�������ɉɂ�����̂́A�悭�Ȃ����Ƃ��v�Ǝv�����t������B �@���w�̋����������F�l����N�ސE���āA���鎄���̒�����т̐i�w�Z�ɍu�t�Ƃ��čďA�E�����B�u�t������A���肮�炢�N���̒S�C�̃T�u�ɂ����B�x�݂����邲�ƂɁu���k�ɏh����o���Ă���v�Ƃ�����B���T�͂R�A�x������A�ċx�ݑO�Łi���k�́j���Ԃ��]���Ă���͂�������c�@���k�Ɏ��R�ɂȂ鎞�Ԃ���������ƁA�낭�Ȃ��Ƃɂ͂Ȃ�Ȃ��Ǝv���Ă���炵���B����ȃX�L�}���Ԃ߂�悤�ȏh��ɁA�q�����������n���A�����Ȃ�悤�ȃG�r�f���X������Ȃ�^�����邪�A���Ԃ����R�ɂԂ����Ȃ��ȊO�ɖړI��������Ȃ��B �@���������A���̏m�ɗ��Ă���q���A���܂�Љ�Ȃɋ����������Ȃ��B�Ȃ����ƕ����ƁA�z����v�����g�̖�肳������Ă����A�_������Ƃ����B�����ɂ��̖����݂��Ă��炤�ƁA�n���̖��Ȃ̂����A�����ËL�����̖�肪�������̃v�����g�ɍ����Ă��āA���\�N���O�̎���ɂȂ��Ă���p��܂ł���B���̐搶�͏m�o�g���ȂƂ����Ɛ��k�͂������Ƃ����Ă����B �@���ꂩ���A�m�ň�����N�オ�搶�ɂȂ�A�e�ɂȂ��Ă����B�����͂��Ă�����͂��Ȃ����낤�B��������l������̓��X�|���X�̑����A�������ʂ��o����A�u���ȏ��������Ă��炤�v����u���ȏ��E���������Ă��炤�v�c�@����ȋ��炪������O���Ƃ݂�Ȃ��v���悤�ɂȂ��Ă����̂��C�ɂ�����B �@�Ȃ��C�ɂ�����̂��Ƃ������R�́A����������Q����B �@��́A�q�ǂ����������Ƃ⋳�ȏ�����ŕ�����Ȃ��Ƃ��낪����l�b�g�i�^�U�̔���͕ʂƂ��āj�Ȃǂ��g���āA�����ǂ���ɂ�����������Ă����ꏊ����������ł����B���ꎩ�̂͊�������Ƃ��B �@�����s�����Ƃ������ґ�ȔY�݂Ȃ̂����A���̒����֗��ɂȂ��āA������Ȃ����́A���炪���Ă�����̂̒��Ŏ����Ă������Ƃ����Ȃ��Ȃ������Ƃł���B�m����Z�p�̑��������Ől�Ԃ͐�������킯�ł͂Ȃ��B�ӎ����ł��낢��ȏ����A�������Ă����Ƃ����f�t�H���g���[�h�l�b�g���[�N�̊��p���K�{���Ǝv���B �@���̐����ȊO�ɂ��A���A�N�^�[�i�������j�̋@�\�������āA�n���͂�A�C�f�A�A�m���E�Z�p�̐[�݂Ɋւ��ƍl���Ă���B�i���A�N�^�[�̔��z�̓E�H���^�[�E�t���[�}���u�]�͂����ɂ��ĐS��n��̂��v����A�S���A�C�f�A���������낤�ƁA�ؗp�����j �@�̂̐l�́A����Ȓm���͒m��Ȃ��������A�l�Ԃɂ͂���Ȕ\�͂�����ƕ������Ă����̂ł͂Ȃ����B �@������A�Â��́A�A���L���f�X�����͂̌����������Ƃ��u�G�E���J�v�Ƃ����ĕ��C���яo�����Ƃ��A�Ђ�߂���A�C�f�A�͔n��A����A�̏�łłĂ���̂��Ƃ����b���r�ꂸ�`����Ă���̂��낤�B���̂悤�ȂЂ�߂���A�C�f�A�́A�ؓ��𗧂Ăē����o�������̂ł͂Ȃ��̂��B �@���z�@��A�C�f�A�֘A�̏��ЁA�Ⴆ�u�A�C�f�A�̂�����v�Ƃ����{�̒��ł������悤�Ȃ��Ƃ������Ă���B�i���҂̓W�F�[���X�E�����O�B���ɖ{�T�C�Y�̂P�O�O�y�[�W�����Ȃ������Ȗ{�����A���ł��P�X�W�W�N�łV�O���ȏ�̒������O�Z���[�B���ł��傫�ȏ��X�ɍs���Ζ{�I�̈�p���m�ۂ��Ă���j �@�m��������������Ƃ����킯�ł͂Ȃ��B���y���āA�n�����Ă����A��������Ɛg�ɂ����̂Ȃ̂��B�������A���̒��̓X�s�[�h�A�����A�𗧂c�@���D�悳��A�����r�W�l�X���[�h�̃^�C���X�p���łōl���镗��������B�ȑO�ɏm�ɗ��Ă������w�����A���ꂩ��ʂ̏m�����邩�瑁���I��肽���Ƃ����B���������̂���u���ƁA�u���ǖ@�v���K���Ă���̂��Ƃ����B�Ԃ����t��������Ȃ������B �@�T���ʼn��\�A���S�y�[�W���ǂ߂�m�������A�����ł��Ȃ��A�������肱�Ȃ��A�Ⴄ��Ȃ����Ƃ����Ȃ���A����u���Ă܂��ǂݕԂ��P�y�[�W�̂ق����͂邩�ɐ����Ɍq�����Ȃ����Ǝv���̂����c�B �@������̗��R�́u������ʂ𑈂��悤�ȕ��͐g���ŏ��ʂ𑈂��̂Ȃ�L�������A����͏ܖ��������ꂩ�����Ă���̂ł͂Ȃ����v�Ƃ����\�z���B �@���{���܂���������ł���A���̂悤�ȕ��ł�����Ă���ꂽ�̂ł��낤�B���{�Љ�͂��łɐ������ォ�琬�n�A�Ђ���Ƃ��Đ��n���}�����ɏk�ݎn�߂Ă���̂�������Ȃ��B �@�������ɂ͑e���ۂ��Ă��悸�͑O�ւƂ����\�͂ł��悩�������A���n���ɂ��k���ő�l�̒m�b��\�͂��K�v�ɂȂ�B �@�������A���{���k�����e��A��l�̒m�b���q�ǂ��̔��z�Ɍ������Ă���̂ł͂Ȃ����B���G�Ȗ������ՂŃ`�[�v�ȉ����@�ɗ��낤�Ƃ���B�f�������f�A�X�s�[�h�����Ă͂₳��Ă��鎞�ゾ���A����Ԃ��A�[���s���A�o���헪�̂Ȃ����f�A�X�s�[�h�̂��߂Ɉ��S���u��u���[�L�����O���ċɗ͌y�������Ԃɏ���Ă���悤�Ȃ��̂��B �@ �@���̂悤�Ȏ���ɐg�ɂ�����͉̂����B���̃T�C�g����낤�Ǝv�������R�̂ЂƂ������ɂ���B �@�������ǂ�ł���N�����w���Ȃ�A���̂��Ƃ����K���ɂ��Ăق����B �u�������l���ɏo�������A������Ȃ����͕̂�����Ȃ��܂܂œ��̒��Ŏ����Ă����B������Ȃ����̂����̒��ɂ���ƁA������Ƃ�����A�������Ƃ��Ȃ���������Ȃ��B���Ԃ������Ă܂�����Ă݂�B����ł�������Ȃ��Ƃ��́A�N���ɐu�������v |
||
| �O�O�S | ���P�M���b�v�͏��w�Z����n�܂��Ă���A�����C�����Ȃ������� �@���P�M���b�v�́A���w�����璆�w���ɂȂ����Ƃ��A�Z��A�����A���E���w�Z�̕���l�����̈Ⴂ�Ȃǂ̍���A����ɔ����V���b�N�̂��Ƃ������B �@���̃T�C�g�̊Ǘ��l�́A���Ɋւ��Ă͏��w�Z�̒��w�N�����肩��A���̉肪����̂ł͂Ȃ����Ǝv���Ă���B �@�����A���w�Z�̊Ԃ͂��ꂪ�ڂɌ�����`�Ō���Ă��Ȃ��B�Z���Ȃ�A�v�Z�����������肵�Ă����A�P���̓��e���͂����藝���ł��Ă��Ȃ��Ă��A���̒P���̖������̏ꂵ�̂��ʼn������Ƃ͂ł���B�������A�m����Z�\�͒蒅���Ă���Ƃ͌�����B����ł�������x�̓_��������B �@�Ȃ��Ȃ�A���w���̊Ԃ͒P�����I��邲�ƂɃe�X�g������̂Łu���̒P���͂����Z�̎�����������v�����Ă��������œ_������B �@��l��l���悭�ώ@����A�U�N���ŎZ���̃e�X�g���X�O�_�ł����Ă����w�ɂȂ�Ε��ϓ_������ŋ�J����Ƃ��A�V�O�_�ł����Ƃ����w���w�͂����������Ƃ������Ƃ�������B�������f����Q�C�R�̗��������B�������A���̗�ɓ��Ă͂܂邩��Ƃ����āA���ꂾ���Ŕ��f�͂��Ȃ��B���k�����̌��t�̒[�X����������Ă����l�q�ȂǑ����I�ɔ��f���Ă���B �i��P�j��Ɋw�m����Z�\���A��Ɋw�ʒP���̒m���ɓ���ւ���Ă��܂��B �@�Ⴆ�A�����Z�E�����Z�̕M�Z�͌������킵�Čv�Z���邪�A�����Z�̕M�Z�͂������Ȃ��B �@�����Z���w���Ƃʼn����̕M�Z������ƁA�������킹���Ɍv�Z���Ă��܂����k���K������B�L���������������Ă���̂��B�u�����ł͂Ȃ��v�ƊԈႢ�����āA����ň��S�Ƃ͂����Ȃ��B���Ƃ��邲�ƂɃ`�F�b�N���Ȃ��Ɖ���������ԈႢ��Ƃ��Ă��܂��B�L���̖͂��ł͂Ȃ��A���ŗ�������̂Ɛg�̂ɓ����Ă��鐔�ʂ̊��o�̖��Ȃ̂��낤�Ǝv���B 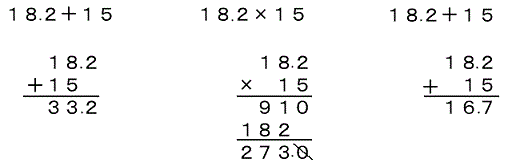 ��i�E�[�̌v�Z���A�����o�����ēǂ܂��Ă݂�B �u���イ�͂��Ă�Ɂ@�����@���イ���@�́@���イ�낭�Ă��@�H�H�H�v �u�N�̌v�Z�ł́A�P�W�ɂP�T�𑫂��ƂP�U�Ɍ�����ȁv (��Q)�@�v�Z�̖���d�g�݂��������Ă��邱�Ƃł��A��ɓ��ɕ������Ƃ�D�悷��B �@�R�O���Q�~�T�@�Ƃ����v�Z������B�v�Z�̏����͑O���炾�B �@�R�O���Q���P�T�@�P�T�~�T���V�T �@�������A�v�Z�̌㔼�ɂ���@�Q�~�T�i�ɂ������イ�j�����ɕ����ԂƁA�v�Z�̏����͂������̒���������āA�R�O���Q�~�T���R�O���P�O���R�@�ƌv�Z���Ă��܂��q�����Ȃ��炸����B���ɕ������Ƃ�D�悵�Ă��܂��B���̂悤�ȌX���͏n��̓ǂ݂ɂ����ʂ��Ă݂���B �@���K�E�{�L���u�����[���Ȃ��̂œǂ߂Ȃ��̂́A��������ނ��Ƃ��B���L�̊����̌�ǗႪ�܂����B�n�ꂪ�ǂ߂Ȃ��Ƃ��́A�ً}���I�Ɂu�����ǂ݁v�œǂ�ł������A�Ƃ����Ă���̂����B �@�@���傼���F���ȂŊw�K�����������u��v���Ƃ��Č����Ƀq�b�g�����B �@���v�@�����߂��F�u���i����j�v����Ɂu�v�v���q�b�g���āA���̒��Łu�v�v�ɘA�Ȃ��b�ōŏ��Ƀq�b�g�����̂��u�����߂��v �@ �@��̗�ȊO�ɂ��A�v�Z�ł́~�̕������Ȃ��̂Ɋ|���Ă��܂��A��������`�◝�_�����o���B�c�@����������肪�Ȃ����A���т����ʂ̐��k�Ɍ��������Ƃł͂Ȃ��B �@�������A�����͌��ۂƂ��ĕ\�Ɍ���Ă���ɉ߂��Ȃ��B�r�������`�Ő��k�̎��Ԃ��ɏ����Ă���̂́A�R���s���[�^�̃v���O�����̂悤�Ɏq�ǂ��͂��̒ʂ�ɂ͓����Ȃ����A�e�⋳�t���o�������ʂ�Ɏq�ǂ��������悤�ɗ������Ă���Ƃ͌���Ȃ��B�����������Ƃ��������Ă��Ȃ��ƁA�D�揇�ʂ�������Ȃ��B �@���w�Z�̎Z�����������肵�Ă���A���̍��Y�Œ��w�Z�̐��w�Ȃ�ŏ��̔��N���炢�́A���Ƃ�����Ă�����͂����B���w�ɂȂ��ċ}�ɐ��w������Ȃ����킯�ł͂Ȃ��B |
||
| �O�O�T | �@��_�˔j �@���̂��Ƃ̗����⏑����Ă��镶�𗝉�����ɂ́A���ʂ���m���A�m�b�A�Z�\���K�v�ł���B���w�������ߒ��ɂ��A�����Ȃɂ��L���Ȓm���Ȃǂ��܂܂�Ă���B �@������A���w�̔\�͂����A����Ɉ���������悤�ɑ����Ȃ̐��т��オ��B����𐔊w�̊w�K�ɂ���Ĉ�_�˔j����Ƃ����B�������A�Љ��ł����p�ł��ŗL�̂��̂����邩��A�����܂ł̓J�o�[�ł��Ȃ��B �@���������B �@������́A���낢��Ȋ�{��g�ݍ��킹�č��B���������قǁA������ɂȂ�B���炪���������Ƃ��ق����悤�ɁA���ݍ�������{���Ƃ��ق������Ƃ��ł���Τ�����̎����������Ă��邩������Ȃ��B���������\�͂͑����ȂɌ��炸�A�������ɂ����p�ł���B �@�����������Ƃ͕������Ɍ��������Ƃł͂Ȃ��B�ǂ̕���ł��A�����l���Ă���l������B�����łȂ���A��_�˔j�Ƃ������t�����܂�Ă��Ȃ������Ǝv���B �u�G���s�c��̂����߁v�i���Ԋ��@�������Ɂj�̒��ʼn�Ƃł��钘�҂́u�悢�d���Ƃ����̂͊�b�̕����ŋ��ʂ�����̂���R����̂ő��̃W�������̎d�����������Ղ��Ƃ������ƂɂȂ邾�낤�v�Ƃ����Ă���B �@������A�����Ƃ������Ƃɂ��āA��������Ă����B �@�u���i�m���Ȃǂ��܂ށj�𗝉�����v�̂ł͂Ȃ��A�u���̗����̎d���𗝉�����v�̂ł���B���^�����Ƃ����āA����ɂ���ė���x�������Əオ��B �@�p���������߂̐��k���ԂԂ����Ȃ���A�p�앶�����Ă���B "Where do..."�͂��邯��ǁA"Where does..."�͕��������Ƃ��Ȃ��̂ŊԈႢ��������Ȃ��B"Where am ..."�͂���킯���Ȃ��B �@What do �� What can ����������������Ŋo���Ă��邩��A�ő��Ɍ��Ȃ����̂͊ԈႢ���ƍl���鐶�k�͌��\������̂��B �@�����ł͂Ȃ��āA��O�͂��邪�AWhat,When,How,What time,How many ..s �Ȃǂ̋^�⎌�̂��Ƃɋ^�╶������̂��A�ƌ�����ς������邾���Ŕ[������q������B �@What do / you have? �ł͂Ȃ��ā@What / do you have? �@�uWhat do �ł͂��܂�^�╶�́c�v�Ƃ����Q�l�����������悤�ɋL�����Ă��邪�A�ǂ��炪�����̂������肩�˂邪�A�����̕��@��������Α����Ȃł��A�d���ɏA���Ă��A�������Ղ��B �u���̐l�́A�d���̈��ݍ��݂������v�Ƃ�����l�́A�d�����̂��̂��o������A���̎d���ǂ��������邩�A�Ƃ������_����X�^�[�g���Ă���̂��Ǝv���B �Ǖ�F�S���w�ł�����u�w�K�̓]�ځv��u���^�F�m�v�Ƃ������_��G�r�f���X���܂��������Ă��Ȃ�����ɂ����āA�u��_�˔j�v�Ƃ������t�ł�����\�����̂ł͂Ȃ����Ǝv���B �@�u�����������̂��v�u�����l����̂��v�u����Ɣ[�������v�Ƃ����o���́A�v�`�u���C�N�X���[�݂����Ȃ��̂��Ǝv���B���ꂪ�d�Ȃ��āA����臒l�����Ƃ���ő傫�Ȕ�҂��Ă���̂��Ǝv���B |
||
| �O�O�U | �@���x���@�V�˂�ڎw�� �@�{�̑т�m�̃`���V�Ɂu�V�˂���Ă�v�Ƃ����R�s�[������̂����܂Ɍ�������B�c�O�Ȃ���A����Ȃ��Ƃ͕s�\�ł���B�V�˂͈�Ă���̂ł͂Ȃ��āA����Ɉ���̂�����ł���B �@��X�}�l���ǂ������������A�u���b�N�z�[���݂����ȓV�˂̓��̒��g��s���������𖾂ł��Ȃ��B���Ԃ�A�{�l���ǂ����Ă����Ȃ�����������Ȃ��̂ł͂Ȃ����B �@�w�͂��_�����w�ыZ�ʂ��ɂ߂Ă��G�˂ɂ͂Ȃ�邪�A�V�ˁE�S�˂Ƃ͌Ă�Ȃ��B�}�l���炷��A�G�˂��_�̏�̐l�ł͂��邪�A���ƂȂ��G�˂��ł��������Ă����ߒ��͗\�z�����B�������A�V�˂͍ŏ�����˂������Ă��邩�A���W���̃u���[�N�X���[���N�����Ĕފ݂Ƀ��[�v���Ă��邩��A�ǂ����Ă����Ȃ�̂��z������ł��Ȃ��B �@�V�˂Ƃ����ƁA�Ő�[�̉Ȋw�Z�p�A�A�[�g�Ȃǂ̕���Ŋ��Ă���l��A���������ʂ�����A�X�P�[���̑傫�Ȑl�����v�������ׂ�B�������A�����Ɛg�߂ȂƂ���ł��A��l�̑n���͂ł͗����ł��Ȃ��˂��������l������͂����B���������l�������V�˂ƌĂ�ł����Ǝv���B���������l�����̘b����l�ł���������A�����������Ȃ����Ǝv�����B �@���Z�ŋΖ����Ă����Ƃ��ɁA�Z�Տ\�i�̓����������B�N���X�̃e�X�g�̏W�v�ƕ��ϓ_�̌v�Z�𗊂��Ƃ�����B�\�̏ォ�牺�܂Ŗڂ�ʂ��Ɠ����Ɍ��ʂ��łĂ���B���Ƃŏ��������Ɣ��Ȃ����B�\�i�͂X���A�P�O���̑����Z�������Ȃ�Ă���B�ނ��猅�̏��Ȃ������Z�͂��ɂ����ƕ��������Ƃ����邵�A�Q���̌v�Z���\�i�ɂ���Ă��炤�͎̂��炾��������ł���B �@�Z�L�i�҂̈ÎZ�͓��̒��Ŏ���͂����Ƃ����B�����̎Q�l�ɂȂ�ƁA���̑��������Z������Ƃ��ɓ��̒��͂ǂ��Ȃ��Ă���̂��Ɛu���Ă݂��B �@�Ⴆ�A���܂ł���X���̐����P�O�����āA����𑫂��Ă����Ƃ��͂ǂ��Ȃ��Ă���̂��Ƃ����ƁA���̂悤�ɐ������Ă��ꂽ�B �@�ォ�瑫���Ă����Ɠ����ɓ��̒��̎Z�Ղ̎삪�����������œ����Ă���̂��������B�����̈ʒu�͖{�l�ɂ�������Ȃ��A�X���b�g�}�V�[���̊G�������邮�����Ă���̃C���[�W�ɋ߂��Ƃ����B�������A�ǂ�ǂ��čŌ�̒i�܂ł���Ă����Ƃ��ɁA�삪�҂����Ǝ~�܂�B���ꂪ�����ɂȂ��Ă���Ƃ����B�c�O�Ȃ���A���k��������q���g�ɂ͂Ȃ�Ȃ������B �@���̘b���v���o���āA�u�V�ˁv�̓��~�b�^�[���O���̂ɐ��������l����Ȃ����ƍl�����B���ʂ̐l�Ԃ͒N�ł��������\�͂������Ă��āA������펞�g���Ɣ]��g�̂����g���Ă��܂�����A���~�b�^�[�ɂ���Ă킴�Ɣ\�͂��������Ă���̂ł͂Ȃ����B �@�Ⴆ�A�Ύ���̔n���͔͂�펞�ɂ����o�Ă��Ȃ��B�����̎����ӂ����ő吺���o���ƁA���傫�Ȑ����o��Ɖ����̖{�œǂL��������B�i�����吺�R���e�X�g�ɉ��p����ΗD������Ǝv���j �@�ق��ɂ��A��X�������Ă���펯�Ƃ������~�b�^�[�����邾�낤�B�吳�̌��������ɁA���̍��̏������ĕU���T�U�S���ł���ʐ^�������B�P�U�U�O�s������R�O�O�s�ɂȂ�B����l�̏펯���猩��A����͕s�\�����A�����̏펯��������\�ɂ��Ă���̂��낤�B���̎���̒S������A�����₷���̂���ɂ��ĂP�U�U�O�L���ƌ��߂��炵���B����l�ɂ͍l�����Ȃ��d�����B �@ �@�ł́A�ǂ�������~�b�^�[���O����̂��낤�B�����A�������D���ł��܂�Ȃ��A�������s���Ȃ��A�����ƒm�肽���A�����Ɠ��������Ƃ�����M���r�������~�b�^�[���O���̂ł͂Ȃ����Ǝv���B �@�������A�������M�������Ă����ɗ��Ƃ��������ׂ���Ƃ��A���̂悤�ȓ��@�ł͌��E��˂��������Ȃ��C������B |
||
| �O�O�V | �@���ꂪ�ʂ����āA�P�A���X�~�X�Ȃ̂� �@�r�������a�P�O�S�ł������G�ꂽ���A�V�����w�v�Z�̖����A����ȑO�̕ʂ̖��Ő��藧���Ă���v�Z�ɓK�p���Ă��܂��B���ɂӂ��ƕ������̂�������l����O�ɏ����Ă��܂����Ƃ��q�ׂ��B �@����ȊO�ɂ��A�v�Z���Ń}�C�i�X�L�������Y���A����ɏ����ׂ������q�ɏ����B�p���ɂ���Ƃ��ɁA������啶���ɂ���̂�Y���A�����̃s���I�h��Y���A�������Ƃ��Ă��镶���Ə����Ă��镶�����Ⴄ�c�@�����グ��Ƃ��肪�Ȃ��B �@�W���͂�������A�Ȃ�Ƃ��Ȃ�ƍl����l�������̂ł͂Ȃ����B���k�͐��k�Łu���͗��K�ŁA�{�Ԃ̃e�X�g�ł͊Ԉ��Ȃ��v�ƌ�������B �@�싅�̎�����K�łڂ�ڂ�G���[�����Ă���I�肪����B�ē�R�[�`�́u�W���͂�������A���Ƃ��Ȃ�v�ƍl���Ȃ��B�G���[���d�˂Ă���I�肪�u�{�Ԃ̎����ł́A�G���[�͂��Ȃ���v�Ƃ����Ă��N���M�p���Ȃ��B����͂����P�ɋZ�p�������Ă��Ȃ������ŁA�W���͂ŋZ�p�̓J�o�[�ł��Ȃ����A���K�łł��Ȃ��������̂��{�Ԃ̎����łł���킯���Ȃ��B �@����e�X�g�̉����āA�_���̂悢���k�ɋ��ʂ��Ă��邱�Ƃ͊�{�̖����Ԉ��Ȃ��B����͓������(�������Z)�ɂ�������B��������������ł͂Ȃ��B�i������Ƃ����̂͊�{�m���̑g�ݍ��킹�𑽂����č���Ă���B�����͂ǂ�����̂��͂܂��ʂ̍��Łj �@�Ղ��������Ԉ��Ȃ��B��{����������������B���ꂾ���Ȃ̂ɃP�A���X�~�X����������B �@�N����ׂ����ċN�������~�X�A�����̃~�X�ɂ͂��ׂČ���������B�P�A���X�~�X�������ɂ���ƁA�������Ȃ̂����ڂ₯�Ă��܂��B �@�r�������`���͎Q�� �@���̃T�C�g�̊Ǘ��l�́A���̂S�̊ϓ_���琶�k�������ςĂ���B�r�������`�Œm���E�Z�\���ŏd�v�Ȃ��Ƃ͊m�������A�S�Ԗڂɂ����̂͂Ȃ����ꂪ���܂������ł��Ȃ��̂��A�Ȃ��蒅���Ȃ��̂��̗��R���P����R�ɂ���ƍl���Ă��邩�炾�B �P�D���t �Q�D���[�L���O�������[�Ɣ]�̂n�r �R�D���A�N�^�[�Ƃ��Ă̔]�A���̑� �S�D�m���E�Z�\ |
||
| �O�O�W | ���ՂɁA����ɈՂ�����������A�ł���悤�ɂȂ�Ƃ͌���Ȃ� �@�ŋ�(2019.Jun)�@���w���w�Ɍ��炸�e���Ȃł��Ղ����A����ɈՂ����A����ł����Ƃ������炢�ɒ��߂������Q�l�������W�̂悤�Ȃ��̂�����ނ��o�ł���Ă���B �@�薼�������ƌ��n���Ɓu�Ƃ��Ă��₳�����E�E�E�v�u���[��Ƃ₳�����E�E�E�v�u�E�E�E�ЂƂЂƂ킩��₷���v�u�z���g�ɂ킩��E�E�E�v�c�@���̂悤�Ȏ�ނ̏��Ђ��������̂́A���ꂾ�����v�����邩�炾�B���̗��R���v�����܂܂ɏ����o���Ă݂�B �@�Ƃŕ����悤�ɂ��A�w�Z�̏h�肪�킩��Ȃ��B �@�ی�҂��Y��Ă��邩��A�������Ă������Ȃ��B �@�w�Z�Ő搶�̐������킩��Ȃ��A�w�Z�ł͕������Ă����͂��������K���悤�Ƃ���ƕ������Ă��Ȃ������B �@���̎Q�l�����A���ؒ��J�ɏ�����Ă���悤�Ɏv������B �@�����ȏ��X�ł̓X�y�[�X�̊W�ł����Ă��͂P�Е����̂悤�Ȗ{���u���Ă���͕̂������Ă������A�傫�ȏ��X�ɍs���ƁA�e�Ђ���o�ł���Ă��āA����ɕ��ς݂ɂȂ��Ă���B������}�ɑ������̂��m��Ȃ������B �@�ق�Ƃ��ɕ������Ȃ�A�c�O�Ȃ��炱���̖{���g���Ă��A���ǂ͕�����Ȃ��܂܂ɏI����Ă��܂���������Ȃ��B �@���ɁA���̎Q�l���̗��̉����������ė����ł��Ĕ[���ł���Ȃ�A���N�x������̃��x���̖��W�Ȃ�Q�l���ł������̂ł͂Ȃ����Ǝv���B �@�����̖��W�͍��ؒ��J�ɉ�����Ă���悤�Ɍ����āA���܂ł̎Q�l���̐�����搶�̐������ׂ�������������ł���B�����̕��������͗����ł��Ă��A�S�̑����A�̗����c���ł��Ă��邩�ǂ������^�킵���̂ł���B�����鑤���������鑤����J���Ă���̂͂��̕����ł���B �@�Ⴆ�A���w�̏ؖ��Ȃǂ́A���t�Ǝ���D������������P�O�s�O�㏑���āA���߂ĂЂƂ̉Ƃ��Ċ����ł���B���̂ЂƂ����܂���u�͂��̂悤�ɂ��ď����v�Ɛ������Ă��A��x�ŗ����ł��鐶�k�͂��������Ȃ��B �@������A�S���炢�̃u���b�N�ɕ����āA�u���b�N���ƂɕK�v�Ȓm���Ȃǂ�������B�������Ȃ����킹��ƉɂȂ邩�Ƃ��������͂����Ȃ��B�����܂��ɉ̌i�F(�v�})�������ŕ`���Ȃ���Ȃ�Ȃ��B �@�O�p�`�̍������ؖ�����ɂ́A�`�a�b�c�̂S�̃u���b�N�ɕ��������̂����ɉ������킯�ł͂Ȃ��B���S�̂����āA�c���琄�����Ă`�ɖ߂�A�ǂ̎O�p�`�̍������ؖ����邩�l����B���̊ԁA�]�͖�肩��킩��f�[�^���獇���������l����B����͂b�ɂ�����B����ɂ���Ăa�ɏ������̂��킩��B�����������X�̂��Ƃ��]�ŏ�������āA���Ă������i�߂���B �@������������m����g�ݗ��Ă�ɂ́A�����̖��ɓ�������A��̖���O��I�ɂ���āA�̍\������������������Ǝv���B�ؖ��̉͂����������̂��A�Ƃ����̂����Ă���ƁA���߂����̂��B �@���╶�͂́A�����邱�Ƃɂ���ĈՂ����͂Ȃ邪�A����őS�̂�������悤�ɂȂ�Ƃ͌���Ȃ��B�S�̑����͂����肵�Ȃ��̂́A��������A������₵����Ԃ͐��_�q����悭�Ȃ��B�������A�����������Ƃ͂��ꂩ�牽�x�ł��K�����̂ŁA�P���Ȃ��Ƃ�����I�ё�����ƁA���n�ł��Ȃ��i��l�ɂȂ�Ȃ��j�B �@���G�Ȃ��̂��ǂ��t�������A����������@�𒆊w���w�̒��ň�������Ǝv��. |
||
| �O�O�X | |||